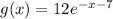Question

PLEASE HELP!! Write an equation of g(x) that represents an exponential base “e” parent function with the following transformations:

Reflect over y-axis, shift right 7, vertical stretch by 12

Answer 1

`g(x) = 12 {e}^( - x - 7)`

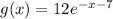
Explanation:

The parent function is

`g(x) = e {}^(x)`

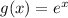
First it is asked to reflect over the y axis so using the rule

`g(x) = g( - x)`

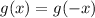
Our function looks like

`g(x) = e {}^( - x)`

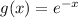
Then we are asked to shift the equation to the right 7. When shifting to the right or move the x axis, instead of adding 7 we would want to subtract 7 since the x axis is the independent variable and we must respect the y axis which is the dependent so using the rule

`g(x) = g(x - h)`

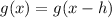
When subtracting a 7 it looks like now

where h is the number we move . Now we are asked to apply a vertical stretch of 12. Since vertical stretch refers to the y axis, we are just going to multiply the function by 12 using the rule

`g(x) = a * g(x)`

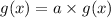
where a is the vertical stretch. So now it would look like

`g(x) = 12 {e}^( - x - 7)`