Question

Use the limit definition of the derivative to find the slope of the tangent line to the curve

f(x)= 7x^2 + 7x + 3 at x= 4

Answer 1

`\displaystyle f'(4) = 63`

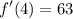
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Distributive Property

Algebra I

• Expand by FOIL (First Outside Inside Last)
• Factoring
• Function Notation
• Terms/Coefficients

Calculus

Derivatives

The definition of a derivative is the slope of the tangent line.

Limit Definition of a Derivative:
`\displaystyle f'(x)= \lim_(h \to 0) (f(x+h)-f(x))/(h)`

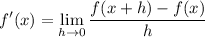
Explanation:

Step 1: Define

f(x) = 7x² + 7x + 3

Slope of tangent line at x = 4

Step 2: Differentiate

1. Substitute in function [Limit Definition of a Derivative]:
   `\displaystyle f'(x)= \lim_(h \to 0) ([7(x + h)^2 + 7(x + h) + 3]-(7x^2 + 7x + 3))/(h)`
2. [Limit - Fraction] Expand [FOIL]:
   `\displaystyle f'(x)= \lim_(h \to 0) ([7(x^2 + 2xh + h^2) + 7(x + h) + 3]-(7x^2 + 7x + 3))/(h)`
3. [Limit - Fraction] Distribute:
   `\displaystyle f'(x)= \lim_(h \to 0) ([7x^2 + 14xh + 7h^2 + 7x + 7h + 3] - 7x^2 - 7x - 3)/(h)`
4. [Limit - Fraction] Combine like terms (x²):
   `\displaystyle f'(x)= \lim_(h \to 0) (14xh + 7h^2 + 7x + 7h + 3 - 7x - 3)/(h)`
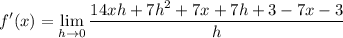
5. [Limit - Fraction] Combine like terms (x):
   `\displaystyle f'(x)= \lim_(h \to 0) (14xh + 7h^2 + 7h + 3 - 3)/(h)`
6. [Limit - Fraction] Combine like terms:
   `\displaystyle f'(x)= \lim_(h \to 0) (14xh + 7h^2 + 7h)/(h)`
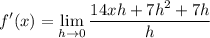
7. [Limit - Fraction] Factor:
   `\displaystyle f'(x)= \lim_(h \to 0) (h(14x + 7h + 7))/(h)`
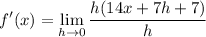
8. [Limit - Fraction] Simplify:
   `\displaystyle f'(x)= \lim_(h \to 0) 14x + 7h + 7`
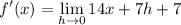
9. [Limit] Evaluate:
   `\displaystyle f'(x) = 14x + 7`

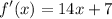
Step 3: Find Slope

1. Substitute in x:
   `\displaystyle f'(4) = 14(4) + 7`
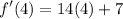
2. Multiply:
   `\displaystyle f'(4) = 56 + 7`
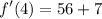
3. Add:
   `\displaystyle f'(4) = 63`

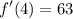
This means that the slope of the tangent line at x = 4 is equal to 63.

Hope this helps!

Topic: Calculus AB/1

Unit: Chapter 2 - Definition of a Derivative

(College Calculus 10e)