Question

If 5.025 grams of NaOH are dissolved in 2.4 liters of water, what is the Molarity of the solution?

Answer 1

0.052 M.

Step-by-step explanation:

Hello!

In this case, since the molarity is computed by dividing the moles of the solute by the volume of the solution in liters (M=n/V), we first need to compute the moles in 5.025 grams of NaOH as shown below:

`n=5.025g*(1mol)/(40.0g)\\\\n=0.126mol`

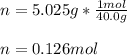
In such a way, we compute the molarity as show below:

`M=(0.126mol)/(2.4L)\\\\M=0.052M`

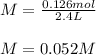
Best regards!