Question

Mr. Crow, the head groundskeeper at High Tech Middle School, mows the lawn along the side of the gym. The lawn is rectangular, and the length is 5 feet more than twice the width. The perimeter of the lawn is 250 feet.a. Define a variable and write an equation for this problem.b. Solve the equation that you wrote in part (a) and find the dimensions of the lawn. c. Use the dimensions you calculated in part (a) to find the area of the lawn.

Answer 1

Given:

Length of the rectangular lawn is 5 feet more than the width.

Perimeter of the lawn is 250 feet.

The objective is,

a) To define the variables and write an equation.

b) To solve the equation in part (a) and find the dimensions of the lawn.

c) To find the area of the lawn.

a)

Consider the width of the lawn as w feet.

It is give that the length of the lawn is 5 feet more than the width of the feet.

Then, length of the law can be represented as, l = w+5.

Since, the perimeter is given as 250 feet, the equation can be represented as,

`\begin{gathered} P=2(l+w) \\ P=2(w+5+w) \\ P=2(2w+5)_{} \\ P=4w+10 \end{gathered}`

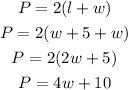
Hence, the required equation is P = 4w+10.

b)

Now, the dimensions of the lawn can be calculated by substituting the value of perimeter in the equation.

`\begin{gathered} 250=4w+10 \\ 4w=250-10 \\ 4w=240 \\ w=(240)/(4) \\ w=60\text{ f}eet \end{gathered}`

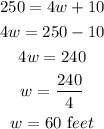
Since, the length of the lawnis 5 feet more than the width of the lawn.

`\begin{gathered} l=w+5 \\ l=60+5 \\ l=65\text{ f}eet \end{gathered}`

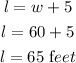
Hence, the width of the lawn if 60 feet and length of the lawn is 65 feet.

c)

Area of rectangluar lawn can be calculated as,

`\begin{gathered} A=l* w \\ A=65*60 \\ A=3900ft^2 \end{gathered}`

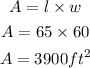
Hence, the area of the lawn is 3900 square feet.