Question

Consider the following function. Complete parts (a) through (e) below.f(x)=x²-2x-8The vertex is.(Type an ordered pair.)c. Find the x-intercepts. The x-intercept(s) is/are(Type an integer or a fraction. Use a comma to separate answers as needed.)d. Find the y-intercept. The y-intercept is(Type an integer or a fraction.)e. Use the results from parts (a)-(d) to araph the quadratic function.

Answer 1

Given the function:

`f(x)=x^2-2x-8`

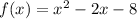
It is a quadratic function where:

a=1

b= -2

c= -8

The x-coordinate of the vertex is given by:

`x=-(b)/(2a)`

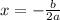
Substitute a and b:

`x=-(-2)/(2(1))=(2)/(2)=1`

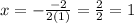
Substituting in the original equation to obtain the y-coordinate, we obtain:

`y=(1)^2-2(1)-8=1-2-8=-9`

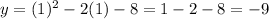
So, the vertex is (0, -9)

c. For the intercept at x we make y = 0:

`0=x^2-2x-8`

And solve for x by factorization:

`\begin{gathered} (x-4)(x+2)=0 \\ Separate\text{ the solutions} \\ x-4=0 \\ x-4+4=0+4 \\ x=4 \\ and \\ x+2=0 \\ x+2-2=0-2 \\ x=-2 \end{gathered}`

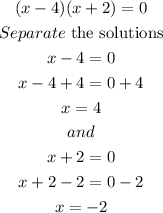
So, the x-intercepts are:

(-2, 0) and (4,0)

Answer: (-2,0), (4,0)

d. For the intercept at y we make x = 0:

`y=(0)^2-2(0)-8=-8`

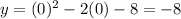
So the y-intercept is (0, -8)

Answer: (0, -8)

e. Graphing the function: