How many ways can a person toss a coin 14 times so that the number of heads is between 6 and 9 inclusive?
the formula of combination is equal to
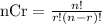
For r between 6 and 9
For r=6
n=14
substitute
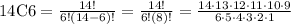
14C6=3,003
For r=7
n=14
substitute
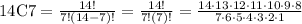
14C7=3,432
For r=8
n=14
substitute
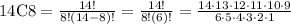
14C8=3,003
For r=9
n=14
substitute
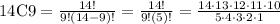
14C9=2,002
adds the combinations
3,003+3,432+3,003+2,002=11,440
11,440 ways