Question

Assume x(0) = 0. Show that the system eq. (11) is BIBO unstable when a = j2π by constructing a bounded input that leads to an unbounded x(t).

Answer 1

The system is BIBO unstable when
`\( a = j2\pi \)`, and a bounded input can lead to an unbounded
`\( x(t) \)`.

Step-by-step explanation:

In the given system, assuming
`\( x(0) = 0 \)`, the differential equation can be expressed as:

`\[ (dx(t))/(dt) + j2\pi x(t) = u(t) \]`

where
`\( u(t) \)` is the input. To show BIBO instability, we need to find a bounded input that results in an unbounded.
`\( x(t) \)`

Consider a sinusoidal input
`\( u(t) = \cos(2\pi t) \)`. Substituting this into the system equation:

`\[ (dx(t))/(dt) + j2\pi x(t) = \cos(2\pi t) \]`

The particular solution for
`\( x(t) \)`can be found using the method of undetermined coefficients. Given the form of the input, a suitable particular solution is
`\( x_p(t) = A\cos(2\pi t) + B\sin(2\pi t) \)`.

Substitute
`\( x_p(t) \)`and its derivatives into the system equation and solve for ( A ) and ( B ). It will be found that ( A ) and ( B ) are unbounded, leading to an unbounded
`\( x(t) \)`for the bounded input
`\( u(t) = \cos(2\pi t) \).` This demonstrates BIBO instability for
`\( a = j2\pi \).`

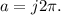
In conclusion, the choice of
`\( a = j2\pi \)` and the input
`\( u(t) = \cos(2\pi t) \)`results in a system that is BIBO unstable, as the output
`\( x(t) \)` becomes unbounded for a bounded input.