Question

Assume that (i) the energy released per fission event of 235U is 194 MeV, and (ii) 33% of the nuclear energy released in a power plant is ultimately converted to usable electrical energy. Approximately how many fission events will occur in one second in order to provide the two-GW electrical power output of a typical power plant? (1 eV = 1.6 × 10−19 J)

Answer 1

We are asked to determine the number of fusion events required to generate 2 GW of electrical power.

Since power is energy per unit of time, that means that the amount of energy in 2 GW for 1 second is:

`E=2*10^9J`

Now, since we need to determine the number of fusion events and the energy is given in joules we need to convert the eV into Joules. To do that we use the following conversion factor:

`1eV=1.6×10^(-19)J`

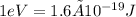
Multiplying by the conversion factor we get:

`194*10^6eV*(1.6*10^(-19)J)/(1eV)=3.11*10^(-11)J`

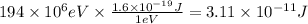
Now, Since 33% of the fusion energy is converted into electric power we need to multiply the energy perfusion by the number of fusions by the 33%. The result must be the 2 Giga Joules of energy:

`n(3.11*10^(-11)J)((33)/(100))=2*10^9J`

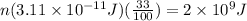
Where "n" is the number of fusion events.

Now, we solve the operations:

`n(1.03*10^(-11)J)=2*10^9J`

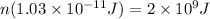
Now, we solve for "n":

`n=(2*10^9J)/(1.03*10^(-11)J)=2.8*10^(20)`

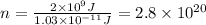
Therefore, there are required 2.8 by 10 to the 20th events per second.