Final Answer:
The value of
 that satisfies the condition where the line through
that satisfies the condition where the line through
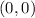 with slope
with slope
 does not intersect the parabola
does not intersect the parabola
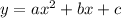 if and only if
if and only if
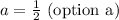 .
.
Step-by-step explanation:
To find the condition where the line
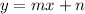 doesn't intersect the parabola
doesn't intersect the parabola
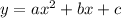 when passing through
when passing through
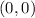 with slope
with slope
 , we consider the discriminant of the quadratic equation formed by their intersection.
, we consider the discriminant of the quadratic equation formed by their intersection.
Given the parabola
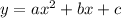 and the line
and the line
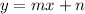 , the point of intersection will satisfy
, the point of intersection will satisfy
 . For
. For
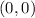 to lie on the line,
to lie on the line,
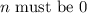 . So, the equation becomes
. So, the equation becomes
 .
.
For the line to not intersect the parabola, the discriminant of this quadratic equation
 must be negative. Here,
must be negative. Here,
 is the coefficient of
is the coefficient of
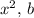 is the coefficient of
is the coefficient of
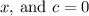 .
.
Solving for the discriminant, we have
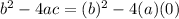 , simplifying to
, simplifying to
 . Since
. Since
 represents the coefficient of
represents the coefficient of
 in the equation
in the equation
 , the condition for no intersection is
, the condition for no intersection is
 .
.
This condition holds true only if
 , implying
, implying
 to satisfy
to satisfy
 . Therefore,
. Therefore,
 is the value for which the line with slope
is the value for which the line with slope
 passing through
passing through
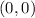 does not intersect the parabola.
does not intersect the parabola.