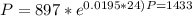Answer:
After next 24 hours, bacterial population would be
Explanation:
The initial bacterial count at time = 0 was
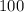
At
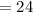 hours, the bacterial count increased up to
hours, the bacterial count increased up to
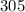
At
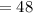 hours, the bacterial count increased up to
hours, the bacterial count increased up to
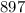
As we know that
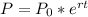
The growth rate of bacterial population is equal to

Substituting the above values we get -
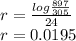
Count of bacteria after next 24 hours