a) 436529 cats b) Approximately 278 years
1) Gathering the data
400,000 cats
Increases yearly by 2.5%
2) Let's write that growth as a function. Note that we must rewrite 2.5% as purely decimal 0.0025. A growth of 2.5 must be written as 1.0025.
Because every time we multiply by 1.0025 we are multiplying the number and 2.5%. Considering that there are currently, in this 1st year 400,000 cats 2036 then this will be 35 years after
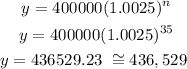
So considering we're in the first year, 35 years after in 2036 there'll be 436,529
b) Since n= is the number of years in that function, and y stands for the number of cats.
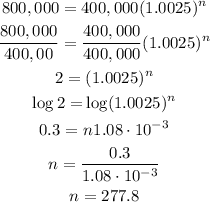
So, it will take at this rate approximately 278 years for the population of cats doubles.