Final Answer:
The density of the rock is approximately 8000 kg/m³.
Therefore, correct option is a) 8000 kg/m³.
Step-by-step explanation:
Find the mass of the rock using the buoyant force.
F = mg
![\[ m = (F)/(g) \]](https://img.qammunity.org/2024/formulas/physics/high-school/85bzdxibonjyqe7d9hwf25g25t2rbwb3po.png)
Given buoyant force, F = 0.021 N, and acceleration due to gravity, g = 9.8
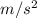 :
:
![\[ m = (0.021)/(9.8) \approx 0.00214 \ kg \]](https://img.qammunity.org/2024/formulas/physics/high-school/n6c8ltypanmac2fmddk4hgm6h3ajerqz58.png)
Use the density formula
 with the known volume of the rock.
with the known volume of the rock.
![\[ \rho = (0.00214)/(2.24 * 10^(-6)) \approx 8035 \ kg/m^3 \]](https://img.qammunity.org/2024/formulas/physics/high-school/g85rtlk31jvs9u93u60y1jqhavau0nmg87.png)
The buoyant force acting on the rock is essentially the weight of the water displaced by the submerged rock. Using the relationship F = mg , we find the mass of the rock. Then, applying the density formula
 , where V is the volume of the rock, we determine the density. In this case, the calculated density is approximately 8035 kg/m³, which rounds to 8000 kg/m³, and this is the density of the rock.
, where V is the volume of the rock, we determine the density. In this case, the calculated density is approximately 8035 kg/m³, which rounds to 8000 kg/m³, and this is the density of the rock.
Therefore, correct option is a) 8000 kg/m³.