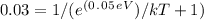Question

find the temperature at which there is 3% probability that a state, with energy 0.05 above the fermi energy will be occupied by an electron.

Answer 1

The temperature at which a state 0.05 eV above the Fermi energy has a 3% occupation probability by an electron can be found using the Fermi-Dirac distribution. This requires solving for T in the expression for the Fermi-Dirac distribution that relates energy, temperature, and occupation probability.

Step-by-step explanation:

To find the temperature at which there is a 3% probability that a state with energy 0.05 eV above the Fermi energy will be occupied by an electron, we can use the Fermi-Dirac distribution function. This function describes the probability F(E) that a state at energy E is occupied by an electron. At T = 0 K, all states with E < EF are filled, while states with E > EF are empty. Nevertheless, at temperatures higher than absolute zero, there is a non-zero probability that states above the Fermi energy are occupied due to thermal excitation.

The Fermi-Dirac distribution function is
`F(E) = 1 / (e^(^E^-^E^F^)^/^k^T + 1)` where k is Boltzmann's constant and T is the temperature in Kelvins. To find the specific temperature at which the occupation probability of the state 0.05 eV above EF is 3%, one must solve for T in the equation
`0.03 = 1 / (e^(^0^.^0^5 ^e^V)/kT + 1)`