The card deck is a standard deck of 52 cards, with 13 cards in each suit.
For the experiment carried out by Michelle, we have the following information:
n(Spades) = 9
n(Hearts) = 11
n(Clubs) = 7
n(Diamonds) = 3
The total number of times she performed the experiment is
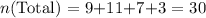
The empirical probability will make use of the experimental results, while the theoretical probability will make use of the total possibilities.
PART A: Empirical Probability of selecting a heart.
Probability is calculated by
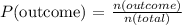
Therefore, the probability is calculated as
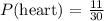
PART B: Theoretical probability of selecting a heart.
This is calculated by
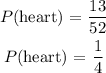
PART C: Empirical probability of selecting a club or diamond.
To calculate the probability for two outcomes, A or B, the probability can be calculated by
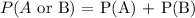
Therefore, we will find the probability of getting a club and then a diamond.
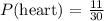
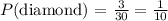
Therefore, the probability of selecting a club or a diamond is

PART D: Theoretical probability of selecting a club or a diamond
We will find the probability of getting a club and then a diamond.
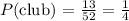
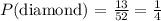
Therefore, the probability of selecting a club or a diamond is
