Question

Solve the equation ( (3cos x - 2)(cos x - 1) ) on the interval . Give the exact solution in radians and an approximation in degrees rounded to the nearest decimal place.

a) 0, (2π); (x = π3), (x ≈ 60^˚)
b) (0, π2); (x = π3), (x ≈ 60^˚)
c) (0, π); (x = π3), (x ≈ 60^˚)
d) (0, 2π); (x = 2π3), (x ≈ 120^˚)

Answer 1

Final Answer:

The correct answer is option (a): (0, 2π); (x = π/3), (x ≈ 60°).

Step-by-step explanation:

The given equation is
`\( (3\cos x - 2)(\cos x - 1) = 0 \).` To find the solutions, we set each factor equal to zero:

1.
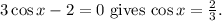
`\(3\cos x - 2 = 0\) gives \(\cos x = (2)/(3)\).`

2.
`\(\cos x - 1 = 0\) gives \(\cos x = 1\)`.

Solving for \(x\) in the first equation, we find
`\(x = \cos^(-1)\left((2)/(3)\)\).`However, since cosine is positive in the first and fourth quadrants, we consider the positive solution, which is
`\(x = (\pi)/(3)\)` in radians.

For the second equation,
`\(\cos x = 1\)`has a solution
`\(x = 0\)`in radians.

So, the solutions in radians are
`\(x = 0\)`and
`\(x = (\pi)/(3)\)`.

To convert radians to degrees, we use the fact that
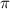`\(\pi\)` radians is equivalent to
`\(180°\)`. Therefore,
`\( (\pi)/(3) \)`in radians is approximately
`\(60°\)`.

Hence, the solutions in degrees are
`\(x = 0\)` and
`\(x \approx 60°\).` Therefore, option (a) is the correct answer.

The correct option:

(a): (0, 2π); (x = π/3), (x ≈ 60°)