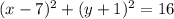Question

Find the equation of the circle that has a diameter with endpoints located at (7,3) and (7,-5). A. (x-7)²+(x+ 1)² = 16 B. (x-7)² + (-1)² =4 C. (x+1)²+(y-7)= 16 D. (x-7)²+(y+ 1)²= 64

Answer 1

The equation of the circle is;

`\mleft(x-7\mright)^2+\mleft(y+1\mright)^2=16`

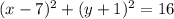
Step-by-step explanation:

Given that the circle has a diameter with endpoints located at (7,3) and (7,-5).

The diameter of the circle is the distance between the two points;

`\begin{gathered} d=\sqrt[]{(7-7)^2+(3--5)^2_{}} \\ d=\sqrt[]{(0)^2+(3+5)^2_{}} \\ d=\sqrt[]{64} \\ d=8 \end{gathered}`

The radius of the circle is;

`\begin{gathered} r=(d)/(2)=(8)/(2) \\ r=4 \end{gathered}`

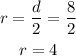
The center of the circle is at the midpoint of the line of the diameter.

`\begin{gathered} (h,k)=((7+7)/(2),(3-5)/(2)) \\ (h,k)=((14)/(2),(-2)/(2)) \\ (h,k)=(7,-1) \end{gathered}`

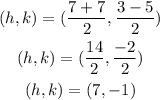
Applying the equation of a circle;

`(x-h)^2+(y-k)^2=r^2`

Substituting the given values;

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ (x-7)^2+(y+1)^2=4^2 \\ (x-7)^2+(y+1)^2=16^{} \end{gathered}`

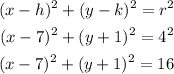
Therefore, the equation of the circle is;

`\mleft(x-7\mright)^2+\mleft(y+1\mright)^2=16`