ANSWER
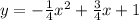
Step-by-step explanation
We want to find the equation for the function graphed.
We see that the function passes through -1 and 4 on the x-axis and 1 is the y-intercept.
These are called the roots of the function. The roots are the x values where the function equals 0.
We can find the function by applying the roots:

where x1 and x2 are the roots.
a = leading coefficient
Therefore, we have that:
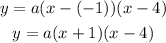
Expand the brackets:
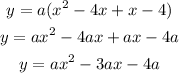
Now, we have to find a.
To do that, we use the y-intercept of the function (0, 1). The y-intercept is the value of the function when x is 0.
Therefore, when x = 0, y = 1:
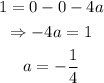
Now, substitute the value of a into the function obtained earlier.

That is the equation of the function graphed.