Question

Please help I have a test on this and I’m not sure how to do this

Answer 1

`y=-(1)/(4)x^2+(3)/(4)x+1`

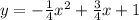
Step-by-step explanation

We want to find the equation for the function graphed.

We see that the function passes through -1 and 4 on the x-axis and 1 is the y-intercept.

These are called the roots of the function. The roots are the x values where the function equals 0.

We can find the function by applying the roots:

`y=a\mleft(x-x_1\mright)\mleft(x-x_2\mright)`

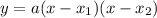
where x1 and x2 are the roots.

a = leading coefficient

Therefore, we have that:

`\begin{gathered} y=a(x-(-1))(x-4) \\ y=a(x+1)(x-4)_{} \end{gathered}`

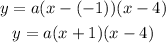
Expand the brackets:

`\begin{gathered} y=a(x^2-4x+x-4) \\ y=ax^2-4ax+ax-4a \\ y=ax^2-3ax-4a \end{gathered}`

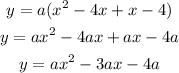
Now, we have to find a.

To do that, we use the y-intercept of the function (0, 1). The y-intercept is the value of the function when x is 0.

Therefore, when x = 0, y = 1:

`\begin{gathered} 1=0-0-4a \\ \Rightarrow-4a=1 \\ a=-(1)/(4) \end{gathered}`

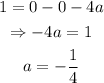
Now, substitute the value of a into the function obtained earlier.

`\begin{gathered} y=-(1)/(4)x^2-3(-(1)/(4))x-4(-(1)/(4)) \\ \Rightarrow y=-(1)/(4)x^2+(3)/(4)x+1 \end{gathered}`

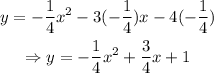
That is the equation of the function graphed.