Final Answer:
The p-value for the test at
![\[ alpha = 0.05} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wg1bolrrh8n8b1002pbxmmdfold3b9sx3b.png) is less than 0.05; therefore, we reject the null hypothesis.
is less than 0.05; therefore, we reject the null hypothesis.
Therefore, option a) 0.05 is correct.
Step-by-step explanation:
To assess whether the data refutes the manufacturer's claim, conduct a one-sample t-test. With a sample mean of 79.7%, a claimed mean of 80%, a sample size of 100, and a standard deviation of 0.8%, calculate the t-statistic.
Using the formula
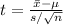 , where
, where
 is the sample mean,
is the sample mean,
 is the claimed mean, s is the standard deviation, and n is the sample size, we find the t-value. Then, find the p-value associated with the t-value.
is the claimed mean, s is the standard deviation, and n is the sample size, we find the t-value. Then, find the p-value associated with the t-value.
With the calculated p-value, compare it to the significance levels
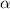 of 0.05, 0.01, 0.10, and 0.20. If the p-value is less than
of 0.05, 0.01, 0.10, and 0.20. If the p-value is less than
 , it suggests that there is sufficient evidence to reject the null hypothesis. In this case, the p-value at
, it suggests that there is sufficient evidence to reject the null hypothesis. In this case, the p-value at
 is less than 0.05, leading to the rejection of the null hypothesis.
is less than 0.05, leading to the rejection of the null hypothesis.
Therefore, option a) 0.05 is correct.