Question

Show the work

Solve for the complex number
1. -2i/1+i
2. i+2/1+i

Solve for the quadratic equation
3. -3x^2+x-3=0
4. 2x^2-4x+7=0

Please help! I would really appreciate it, I honestly don’t understand this.

Answer 1

1. -1-i
2. (3 -i)/2
3. (1 ±i√35)/6
4. (2 ±i√10)/2

Explanation:

There is a special quadratic form called "the difference of squares" that has useful application in a number of situations. The form is ...

a² -b² = (a -b)(a +b)

This means that expressions where 'a' or 'b' are imaginary numbers or radicals can be simplified by using a factor that results in those values being squared.

For a rational expression with a complex number in the denominator, you can make the denominator be a real number by multiplying numerator and denominator by a factor that looks like the denominator, but with the opposite sign.

1.

`(-2i)/(1+i)=(-2i)/(1+i)\cdot(1-i)/(1-i)=(-2i(1-i))/(1^2-i^2)\\\\=(-2i+2i^2)/(1-(-1))=(-2i+2(-1))/(2)=(-2-2i)/(2)=\boxed{-1-i}`

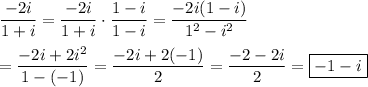
For the most part, the value "i" can be treated as though it were any variable. Like terms add and subtract the way they always do. Products are formed in the usual way. The only difference is that i² = -1, so any time you see that power of i, you can replace it with -1. Similarly, any time you see √(-1), you can replace it with i.

__

2.

(i+2)/(1+i) = (2+i)(1-i)/(1² -i²) = (2 -i -i²)/2 = (3 -i)/2

__

3.

The quadratic formula can be used to solve these. It tells you the solution to ...

ax² +bx +c = 0 is ...

`x=(-b\pm√(b^2-4ac))/(2a)`

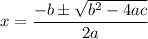
You have a = -3, b = 1, c = -3, so the solutions are ...

`x=(-1\pm√(1^2-4(-3)(-3)))/(2(-3))=(1\pm√(1-36))/(6)=\boxed{(1\pm i√(35))/(6)}`

__

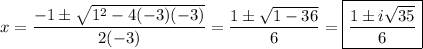
4.

You have a = 2, b = -4, c = 7, so the solutions are ...

`x=(-(-4)\pm√((-4)^2-4(2)(7)))/(2(2))=(4\pm√(16-56))/(4)=\boxed{(2\pm i√(10))/(2)}`

_____

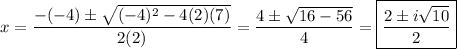
Additional comment

Sometimes answer checkers don't like parentheses. This means you might need to write out the sums.

(3 -i)/2 = 3/2 -1/2i

(2±i√10)/2 = 1+i√10/2, 1-i√10/2 . . . . the /2 is outside the radical