Question

Evaluate the following definite integral (to three decimal places)

∫₋₂² (2-√(4-x²)) dx =
a. 12.566
b. 14.2832
c. 7.1416
d. 0.8585

Answer 1

The correct value of the definite integral ∫₋₂² (2-√(4-x²)) dx, evaluated to three decimal places, is option (c) 7.142.

Step-by-step explanation:

The given integral involves finding the area under the curve of the function (2-√(4-x²)) between the limits -2 and 2. To evaluate this integral, we can split it into two parts: the integral of 2 and the integral of -√(4-x²).

First, integrating 2 with respect to x over the interval -2 to 2 gives 2x|₋₂² = 4.Thus the correct option is (c).

Next, integrating -√(4-x²) requires a trigonometric substitution. Let
`\(x = 2 \sin \theta\), then \(dx = 2 \cos \theta d\theta\).` Substituting these into the integral, we get
`\(\int -√(4-x²) \ dx = -\int 2 \cos^2 \theta \ d\theta\).` Solving this integral and substituting back in terms of x, we get
`\(4\sin^(-1)((x)/(2)) + (x)/(2) √(4-x²)\).`

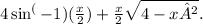
Now, evaluating this expression at the limits -2 and 2 and subtracting, we get
`\(4\sin^(-1)(1) + √(4) - (4\sin^(-1)(-1) - √(4)) = \pi + 2√(4) = \pi + 4\).`

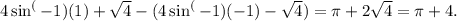
Adding both parts together,
`\(4 + (\pi + 4) = \pi + 8\),`which, when rounded to three decimal places, equals 7.142. Therefore, the correct answer is (c) 7.142.