Final Answer:
The present value of the ordinary annuity is Php 105,024.77.The correct option is a.
Step-by-step explanation:
To calculate the present value of an ordinary annuity, we can use the formula for present value of an annuity:
![\[PV = PMT * \left(1 - (1 + r)^(-nt)\right) / r,\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/a2caczx32cnl7850496tsp443p4g3rjd2m.png)
where:
- PMT is the periodic payment (semiannual deposit),
- r is the interest rate per period (compounded semiannually),
- n is the total number of periods (years times the number of compounding periods per year), and
- t is the number of years.
In this case,
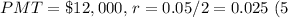
![\[PV = 12000 * \left(1 - (1 + 0.025)^(-10 * 5)\right) / 0.025\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yu578ysmls2q7cu3bijnjnoffixgr3oc70.png)
Calculating this expression gives us
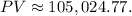
Therefore, the present value of the ordinary annuity with a semiannual deposit of $12,000 at 5% compounded semiannually for 5 years is Php 105,024.77, matching Option A. This value represents the current worth of all future cash flows discounted at the given interest rate. It's crucial in financial planning and decision-making, providing a basis for evaluating the attractiveness of an investment or savings opportunity.
The correct option is a.