Answer: The half-life of the compound is 93 minutes
Step-by-step explanation:
Expression for rate law for first order kinetics is given by:
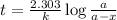
where,
k = rate constant
t = age of sample
a = let initial amount of the reactant =100
a - x = amount left after decay process = (100-36) = 64
a) for completion of 36 % of reaction
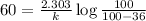
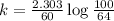
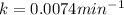
b) for completion of half life:
Half life is the amount of time taken by a radioactive material to decay to half of its original value.
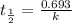
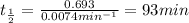
The half-life of the compound is 93 minutes