Question

Assume that ? is a positive acute angle. Given: cos?=725 Find: sin 2?

Answer 1

`\[ \text{Given } \cos \theta = (7)/(25), \text{ we can find } \sin 2\theta \text{ as follows: } \sin 2\theta = 2\sin \theta \cos \theta = 2 * (24)/(25) * (7)/(25) = (336)/(625). \]`

Step-by-step explanation:

In the given problem, we are provided with the information that
`\(\cos \theta = (7)/(25)\)`, where
`\(\theta\)` is a positive acute angle. To find
`\(\sin 2\theta\)`, we can use the double-angle identity for sine, which states that
`\(\sin 2\theta = 2\sin \theta \cos \theta\).`

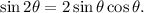
Breaking down the expression, we substitute
`\(\cos \theta = (7)/(25)\)`into the formula. Therefore,
`\(2\sin \theta \cos \theta = 2 * (\sin \theta * 7)/(25)\)`. Now, we need to find
`\(\sin \theta\).` Since
`\(\theta\)` is a positive acute angle, we can use the fact that
`\(\sin \theta = √(1 - \cos^2 \theta)\)`. Plugging in the given value of
`\(\cos \theta\), we get \(\sin \theta = \sqrt{1 - \left((7)/(25)\right)^2} = (24)/(25)\).`

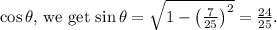
Now, substituting this value back into the expression,
`\(2 * (24)/(25) * (7)/(25) = (336)/(625)\).` Therefore, the final answer is
`\(\sin 2\theta = (336)/(625)\)`, and this is the solution to the given problem.