Question

The weight of football players is normally distributed with a mean of 200 pounds and a standard deviation of 25 pounds. If a random sample of 35 football players is taken, what is the probability that that the random sample will have a mean more than 210 pounds?

Answer 1

We know that

• The mean is 200 pounds.

,

• The standard deviation is 25 pounds.

,

• The random sample is 35.

First, let's find the Z value using the following formula

`Z=(x-\mu)/(\sigma)`

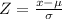
Let's replace the mean, the standard deviation, and x = 210.

`Z=(210-200)/(25)=(10)/(25)=0.4`

Then, using a p-value table associated with z-scores, we find the probability

`P(x>210)=P(Z>0.4)=0.1554`

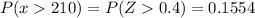
Therefore, the probability is 0.1554.

The table used is shown below