Final Answer:
The height of the missile after 5 seconds in the air is 97 feet.
Step-by-step explanation:
To find the height of the missile after 5 seconds, substitute x = 5 into the quadratic function
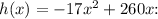
![\[h(5) = -17(5)^2 + 260(5)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/romdunl8wpgzag6kp8kke9xdix8fto9imq.png)
Simplifying this expression yields the height after 5 seconds, which is 97 feet. The quadratic function
 represents the missile's height as a function of time, with the term
represents the missile's height as a function of time, with the term
 capturing the effect of gravity. The coefficient of
capturing the effect of gravity. The coefficient of
 is negative, indicating a downward-opening parabola. The positive term
is negative, indicating a downward-opening parabola. The positive term
 represents the initial upward velocity of the missile.
represents the initial upward velocity of the missile.
By evaluating the function at
 , we determine the height at that specific time. In this case, after 5 seconds, the missile is 97 feet in the air. The negative value of the quadratic term dominates as time progresses, leading to a decrease in height and reflecting the influence of gravity on the missile's trajectory.
, we determine the height at that specific time. In this case, after 5 seconds, the missile is 97 feet in the air. The negative value of the quadratic term dominates as time progresses, leading to a decrease in height and reflecting the influence of gravity on the missile's trajectory.