Question

Point D is in the interior of

Answer 1

The given problem can be exemplified in the following diagram:

The conditions are:

`\begin{gathered} m\angle ABD=6x+5 \\ m\angle ABC=10x+7 \\ m\angle DBC=36 \end{gathered}`

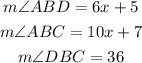
We also have the following relationship:

`m\angle ABD+m\angle DBC=m\angle ABC`

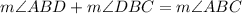
Substituting the values we get:

`6x+5+36=10x+7`

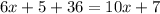
Solving the operations:

`6x+41=10x+7`

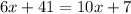
Now we solve for "x", first by subtracting 10x on both sides:

`\begin{gathered} 6x-10x+41=10x-10x+7 \\ -4x+41=7 \end{gathered}`

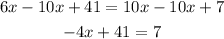
Now we subtract 41 on both sides:

`\begin{gathered} -4x+41-41=7-41 \\ -4x=-34 \end{gathered}`

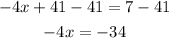
Now we divide both sides by -4

`x=-(34)/(-4)=(17)/(2)`

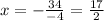
Now we replace the value of "x" in the expression for angle ABD:

`\angle ABD=6x+5`

Replacing the value of "x":

`\angle ABD=6((17)/(2))+5`

Solving the operations:

`\angle ABD=3(17)+5=56`

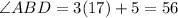
Therefore angle ABD is 56 degrees.