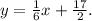Question

Which equation represents the line that contains the point (12, 4) and is perpendicular to the line represented by y = – 6x + 5? *

Answer 1

The equation representing the line that contains the point (12, 4) and is perpendicular to the line y = –6x + 5 is
`\(y = (1)/(6)x + (17)/(2).\)`

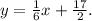
Step-by-step explanation:

To find the equation of a line perpendicular to y = –6x + 5 and passing through the point (12, 4), we need to determine the slope of the given line. The given line has a slope of -6. The negative reciprocal of -6 is
`\((1)/(6)\)` , which is the slope of any line perpendicular to it.

Now, we can use the point-slope form of a linear equation,
`\(y - y_1 = m(x - x_1),\)` where
`\((x_1, y_1)\)` is a point on the line and \(m\) is the slope.

Plugging in the values, we get
`\(y - 4 = (1)/(6)(x - 12).\)`

To simplify, multiply both sides by 6 to get rid of the fraction: (6(y - 4) = x - 12.)

Distribute on the left side: (6y - 24 = x - 12.)

Isolate (y) by adding 24 to both sides: (6y = x + 12.)

Divide by 6:
`\(y = (1)/(6)x + 2.\)`

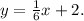
The final equation representing the line perpendicular to y = –6x + 5 and passing through (12, 4) is
`\(y = (1)/(6)x + (17)/(2).\)`