Question

A gas contained in a steel tank has a pressure of 1.5 atm at a temperature of 177°C. What will be the gas pressure when the temperature changes to 47°C?

Answer 1

Using Gay-Lussac's Law, the final pressure of the gas when cooled from 177°C to 47°C is calculated by converting temperatures to Kelvin, then using the proportionality of pressure and temperature. The final pressure is determined to be approximately 1.067 atm.

Step-by-step explanation:

To determine the change in pressure of a gas when temperature changes, while volume and amount of gas remain constant, we can use Gay-Lussac's Law, which is part of the gas laws. This law states that the pressure of a gas is directly proportional to its absolute temperature (measured in Kelvin), as long as the volume and amount of gas remain constant.

The formula derived from this law is:

`\( (P_1)/(T_1) = (P_2)/(T_2) \)`

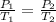
Where:

`\( P_1 \)` is the initial pressure,

`\( T_1 \)` is the initial temperature in Kelvin,

`\( P_2 \)` is the final pressure,

`\( T_2 \)` is the final temperature in Kelvin.

To solve for
`\( P_2 \)`, we rearrange the formula as follows:

`\( P_2 = P_1 * (T_2)/(T_1) \)`

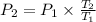
Step 1: Convert temperatures from Celsius to Kelvin by adding 273.15.

`\( T_1 = 177^(\circ)C + 273.15 = 450.15 K \)`

`\( T_2 = 47^(\circ)C + 273.15 = 320.15 K \)`

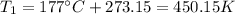
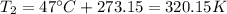
Step 2: Substitute the known values into the rearranged formula and solve for
`\( P_2 \).`

`\( P_2 = 1.5 \ atm * (320.15 K)/(450.15 K) \)`

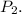
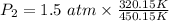
Step 3: Calculate to find the final pressure.

`\( P_2 = 1.5 \ atm * 0.7111 = 1.067 \ atm \)`

So, the pressure of the gas at 47°C will be approximately 1.067 atm.