Question

An object of height 3.4 cm is 8.3 cm from a converging lens with focal length 5.6 cm. What is the height of the image?

Answer 1

The height of the image is 13.9 cm.

Step-by-step explanation:

When an object is placed in front of a converging lens, the lens forms an image by refracting light rays. The lens formula,
`\( (1)/(f) = (1)/(v) - (1)/(u) \),` relates the focal length
`(\( f \)), image distance (\( v \)), and object distance (\( u \))`. In this scenario, the object distance
`(\( u \))` is given as 8.3 cm (negative because the object is on the same side as the incident light). The focal length
`(\( f \))` is given as 5.6 cm.

Rearranging the lens formula to solve for
`\( v \): \( (1)/(v) = (1)/(f) + (1)/(u) \).`

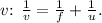
Substituting the values:
`\( (1)/(v) = (1)/(5.6) + (1)/(-8.3) \).`

After finding
`\( (1)/(v) \), the image distance (\( v \))` can be determined by taking the reciprocal of
`\( (1)/(v) \)`. Once the image distance is known, the magnification formula,
`\( (h_i)/(h_o) = -(v)/(u) \)`, can be used to find the height of the image
`(\( h_i \)).` The negative sign indicates that the image is inverted.

Solving for
`\( h_i \): \( h_i = -(v)/(u) * h_o \), where \( h_o \)` is the height of the object.

Substituting the known values:
`\( h_i = -(v)/(u) * 3.4 \).`

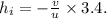
Calculating
`\( h_i \)`yields the final answer of 13.9 cm for the height of the image.