Question

The population of a certain species of owl at a wildlife preserve can beapproximated by the functionN(t) =20401+39e-0.51where N(t) represents the number of owls and t is the time (in years).a.) What was the initial population of the owls?b.) How many owls will there be in the wildlife preserve in the long run? Inother words, what is the limit as t approaches infinity?c.) how many years will it take until there are 950 owls in the wildlife preserve?

Answer 1

Question A.

The initial population ocurrs at t=0. Then, by substituting this value into the given model ,we get

`N(0)=(2040)/(1+39e^0)`

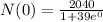
which gives

`\begin{gathered} N(0)=(2040)/(1+30) \\ N(0)=(2040)/(40) \\ N(0)=51 \end{gathered}`

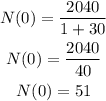
then, the answer is 51 owls.

Question B.

The limits when t approaches to + infinity is

`\begin{gathered} N(0)=(2040)/(1+39e^(-\infty)) \\ N(0)=(2040)/(1+0) \\ N(0)=(2040)/(1)=2040 \end{gathered}`

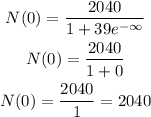
then, the answer is 2040 owls.

Question 15.

In this case, we need to find t when N(t) is 950, that is,

`950=(2040)/(1+39e^(-0.5t))`

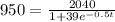
By moving the denominator to the left hand side, we have

`(1+39e^(-0.5t))950=2040`

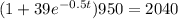
then, by moving 950 to the right hand side, we obtain

`\begin{gathered} (1+39e^(-0.5t))=(2040)/(950) \\ 39e^(-0.5t)=(2040)/(950)-1 \end{gathered}`

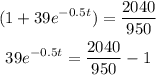
which is

`39e^(-0.5t)=1.147368`

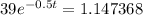
so, we get

`\begin{gathered} e^(-0.5t)=(1.147368)/(39) \\ e^(-0.5t)=0.029419 \end{gathered}`

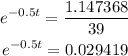
By applying natural logarithms to both sides, we have

`\begin{gathered} -0.5t=\ln (0.029419) \\ t=(-\ln(0.029419))/(0.5) \end{gathered}`

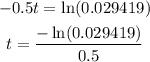
then, the answer is

`t=7.05`

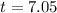
By rounding o the neares interger, the answer is 7 years