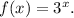Final Answer:
 { is reflected over the x-axis, the equation of the new graph is }
{ is reflected over the x-axis, the equation of the new graph is }
![\boxed{\text{C. } G(x) = - (1/3)^x}. \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/mia6z2xp94jowum2vaeyn319gbzciu4rjc.png) opiton.c
opiton.c
Step-by-step explanation:
When a function is reflected over the x-axis, each y-coordinate of the points on the original graph becomes its opposite. In the case of
 reflecting over the x-axis transforms it into
reflecting over the x-axis transforms it into
 However, the options are in terms of the base, so we need to express
However, the options are in terms of the base, so we need to express
 using the base
using the base
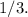
Recall that
 So, to obtain the equivalent expression with a negative sign, we get
So, to obtain the equivalent expression with a negative sign, we get
 . Therefore, the correct answer is
. Therefore, the correct answer is
 corresponding to option C.
corresponding to option C.
In summary, reflecting a function over the x-axis negates the original function, and in this case, expressing it in terms of the base
 gives us the correct transformed function. Thus, option C,
gives us the correct transformed function. Thus, option C,
 is the accurate equation for the reflected graph of
is the accurate equation for the reflected graph of