Question

6. When a company receives an order, there is a probability of 0.42 that its value is over $1000. If an order is valued at over $1000, then there is a probability of 0.63 that the customer will pay with a credit card. a. What is the probability that the next three independent orders will each be valued at over $1000

Answer 1

0.074088

Explanation:

Let

A:Value of order over $1000

B:Customer pay with credit card

We are given that

Probability of value of order over $1000,P(A)=0.42

If an order is valued at over $1000, then the probability that the customer will pay with a credit card, P(B/A)=0.63

We have to find the probability that the next three independent orders will each be valued at over $1000

We know that

When two two events A and B are independent then

`P(A\cap B)=P(A)\cdot P(B)`

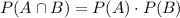
Using the formula

The probability that the next three independent orders will each be valued at over $1000=
`0.42* 0.42* 0.42`

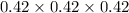
The probability that the next three independent orders will each be valued at over $1000=0.074088