Question

if triangle ABC has sides of length 9, 15, and 3x, between which two numbers must the value of x lie?

Answer 1

Let's employ the triangle inequality here.

If the sides were to form a triangle.

Then if 3x was the longest side, it must be less than the sum of 15 and 9, being the other 2 sides.

So;

`\begin{gathered} 3x<15+9 \\ 3x<24 \\ x<8 \end{gathered}`

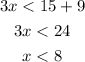
If 3x was the shortest side, then 15 would be the longest side, and thus

3x plus 9 must be greater than 15,

So;

`\begin{gathered} 3x+9>15 \\ 3x>15-9 \\ 3x>6 \\ x>2 \end{gathered}`

So, the range of values for which x must lie is;

[tex]2i.e any values greater than 2 but less than 8.