Final Answer:
The energy E as a function of the temperature
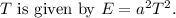
Step-by-step explanation:
To derive the relationship between energy E and temperature T from the entropy expression
 , we start by squaring both sides to eliminate the square root:
, we start by squaring both sides to eliminate the square root:
 . Next, differentiate both sides with respect to temperature T :
. Next, differentiate both sides with respect to temperature T :
![\[ 2S (dS)/(dT) = a (dE)/(dT) \]](https://img.qammunity.org/2024/formulas/physics/high-school/vjqumq1cny8lis7qz7g9uimce99la4fq0n.png)
Now, substitute
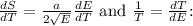
![\[ 2S \left((a)/(2√(E)) (dE)/(dT)\right) = a (dE)/(dT) \]](https://img.qammunity.org/2024/formulas/physics/high-school/dy0w7fk8s7g54a9xz9skiql04s40b1glif.png)
Simplify and integrate:
![\[ S √(E) = (a)/(2) \ln\left((E)/(E_0)\right) \]](https://img.qammunity.org/2024/formulas/physics/high-school/ftg95knm6pg54pgnbwpvx4891sxn6o32yh.png)
Solve for
 to obtain the final result:
to obtain the final result:
![\[ E = a^2 T^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/fjgihg2ipmrohnjmzlpt1s2u86zdp8z7gi.png)
This demonstrates that the energy of the substance is proportional to the square of the temperature.