Question

What is the growth factor in the exponential equation y=4(1.03)^x?

Answer 1

The growth factor in the exponential equation
`y=4(1.03)^x is 1.03.`

Step-by-step explanation:

In the given exponential equation,
`y=4(1.03)^x`, the growth factor is the base of the exponent, which is 1.03. The growth factor represents the factor by which the function's value increases with each unit increase in the independent variable (x). In this case, the base of 1.03 indicates that for each unit increase in x, the function value (y) will be multiplied by 1.03, leading to exponential growth.

To further understand, let's consider an example. If x is 1, then
`y=4(1.03)^1=4(1.03)=4.12`. If x is 2, then
`y=4(1.03)^2=4(1.0609)=4.24`, and so on. The growth factor of 1.03 signifies a 3% increase with each unit change in x. This compounding effect results in exponential growth over successive values of x.

It's important to note that a growth factor greater than 1 indicates growth, while a growth factor less than 1 would signify decay in an exponential equation. In this context, the growth factor of 1.03 points to positive exponential growth.

Answer 2

The growth factor in the exponential equation
`y = 4(1.03)^(x)` is 1.03.

Step-by-step explanation:

In the equation
`y = 4(1.03)^(x)`, the growth factor is represented by the base value 1.03 raised to the power of x.

Let's consider a few values of x to demonstrate the calculation of y and the impact of the growth factor:

When x = 0:

`y = 4(1.03)^0`

y = 4 * 1

y = 4

When x = 1:

`y = 4(1.03)^1`

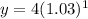
y = 4 * 1.03

y = 4.12

When x = 2:

`y = 4(1.03)^2`

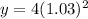
y = 4 * 1.0609

y = 4.2436

As x increases, the growth factor (1.03) raised to the power of x influences the value of y multiplicatively. For instance, when x = 2, the growth factor of 1.03 is squared, resulting in a value of 1.0609, which, when multiplied by the initial value of 4, yields 4.2436.

This showcases how the growth factor of 1.03 operates in the exponential equation. For each increment in x, the growth factor, compounded by exponentiation, leads to an increasing rate of change in the resultant value of y. The larger x becomes, the greater the effect of this growth factor on the exponential growth of the function.