Question

Question :

Two cargo ships spot a signal fire on a small island. The captains know they are 140 feet

away from each other and using angle measuring device they can determine the angle from

each of their ships to the signal fire. The angle at ship A is 82º and the angle at ship B is 78º.

How far is it from Ship B to the signal fire at point C?

Hint: Use Law of Sines:

sin A = simb = sin

82

140 it

A(48.9) b(400.4) C(405.3) D(673.4)

Answer 1

C) 405.3 ft

Explanation:

A triangle is a polygon with three angles and three sides. Types of triangle are scalene, isosceles, equilateral, right angled triangle.

Given a triangle with angles A, B, C and the corresponding sides directly opposite to the angles as a, b, c. The sine rule states that:

`(a)/(sin(A))= (b)/(sin(B)) =(c)/(sin(C))`

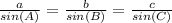
In the triangle formed by point C, ship B and ship A, we have ∠A = 82°, ∠B = 78°, c = AB = 140 ft. Hence:

∠A + ∠B + ∠C = 180° (sum of angles in a triangle)

82 + 78 + ∠C = 180

∠C + 160 = 180

∠C = 20°

Using sine rule:

`(c)/(sin(C))=(a)/(sin(A))\\\\(140)/(sin(20))=(a)/(sin(82))\\\\a= (140*sin (82))/(sin(20))\\\\a=405.3\ ft`

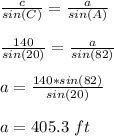
a = distance from Ship B to the signal fire at point C