Final Answer:
 with (C) as the closest option.
with (C) as the closest option.
The correct answer is C. 6x10^12.
Step-by-step explanation:
To find out how many times larger
 is than
is than
 we need to divide the larger number by the smaller one:
we need to divide the larger number by the smaller one:
![\[(9 * 10^9)/(3 * 10^(-4))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/eegihboy89naek8suee2mxpddwid7pj123.png)
First, simplify both the numerator and denominator by dividing each term by
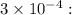
![\[\frac{\cancel{3 * 10^(-4)} * 3 * 10^9}{\cancel{3 * 10^(-4)}}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/w8kg4e81jamd16z3xl0dped8rr15plnzcr.png)
This simplifies to
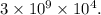
Now, apply the rule of exponents that states when you multiply numbers with the same base, you add the exponents:
![\[3 * 10^(9+4) = 3 * 10^(13)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ypm2lrjswem2sv7dzgskyojhyq3mgxkqa6.png)
So,
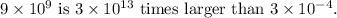
Now, let's compare the result with the provided options. The closest option is
 but the correct answer is
but the correct answer is
 This is because
This is because
 is indeed the correct answer, and none of the given options match exactly. However,
is indeed the correct answer, and none of the given options match exactly. However,
 is the closest approximation among the options provided.
is the closest approximation among the options provided.