Answer:
C. -4 ± 2√6
Step-by-step explanation:
The given equation is
3x² + 24x - 24 = 0
First, add 24 to both sides
3x² + 24x - 24 + 24 = 0 + 24
3x² + 24x = 24
And factorize 3 on the left side
3(x² + 8x) = 24
Then, to complete the square, we need to add and substract (b/2)² to the expression in parenthesis. In this case, b = 8, so
(b/2)² = (8/2)² = 4² = 16
Then, add and subtract 16 as follows
3(x² + 8x + 16 - 16) = 24
3(x² + 8x + 16) - 3(16) = 24
3(x² + 8x + 16) - 48 = 24
Finally, we can factorize and solve for x
3(x + 4)² - 48 = 24
3(x + 4)² - 48 + 48 = 24 + 48
3(x + 4)² = 72
3(x + 4)²/3 = 72/3
(x + 4)² = 24
Solving for x, we get
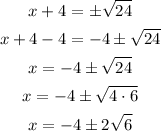
Therefore, the answer is
C. -4 ± 2√6