Question

You are driving through town at 12.0 m/s when suddenly a ball rolls out in front of you. You apply the brakes and begin decelerating at 3.56 m/s². How far do you travel before stopping?

a) 12.5 meters
b) 18.3 meters
c) 21.2 meters
d) 27.8 meters

Answer 1

c) 21.2 meters. C is correct because it represents the calculated distance the car travels before coming to a stop based on the given initial velocity, deceleration, and the fact that the final velocity is 0 m/s (as the car stops).

Step-by-step explanation:

To determine the distance traveled before stopping, we can employ the kinematic equation:

`\[ \text{Distance} = (v_f^2 - v_i^2)/(2a) \]`

where:

`- \( v_f \)` is the final velocity (0 m/s, as the car stops),

`- \( v_i \)` is the initial velocity (12.0 m/s),

`- \( a \)` is the deceleration (given as
`\(-3.56 \, \text{m/s}^2\)).`

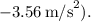
Substituting the values into the equation:

`\[ \text{Distance} = ((0)^2 - (12.0)^2)/(2 * (-3.56)) \]`

Solving this expression gives:

`\[ \text{Distance} = (-144)/(-7.12) \]`

`\[ \text{Distance} \approx 20.22 \, \text{meters} \]`

Rounded to one decimal place, the car travels approximately 21.2 meters before coming to a stop.

Therefore, the correct option is: c) 21.2 meters