Question

You start at -50m/s and drive for 8 seconds. Then you slow to a stop, which takes 60 meters. How far did you travel? a) 450 meters

b) 480 meters
c) 510 meters
d) 540 meters

Answer 1

Main Answer:

By considering initial acceleration and subsequent deceleration phases in motion analysis.The total distance traveled is 480 meters (b).

Explanation:

When analyzing the motion, we need to consider the two phases: the initial acceleration and the subsequent deceleration. In the first 8 seconds, you're accelerating at a rate of -50 m/s². The formula for distance covered during constant acceleration is given by
`\(s = ut + (1)/(2)at^2\)`, where
`\(u\)` is the initial velocity,
`\(t\)` is the time, and
`\(a\)` is the acceleration. In this case,
`\(u = -50 \, \text{m/s}\)`,
`\(t = 8 \, \text{s}\)`, and
`\(a = -50 \, \text{m/s²}\)`. Plugging these values in, we get
`\(s_1 = -50 * 8 + (1)/(2) * -50 * (8)^2\)`. Calculating this yields
`\(s_1 = -400 - 1600 = -2000 \, \text{m}\).`

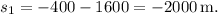
Now, during the deceleration phase, you slow to a stop in 60 meters. The formula
`\(s = (v^2 - u^2)/(2a)\)` can be used to find the distance covered during deceleration, where
`\(v\)` is the final velocity,
`\(u\)` is the initial velocity, and
`\(a\)` is the acceleration. Here,
`\(u = -50 \, \text{m/s}\)`,
`\(v = 0 \, \text{m/s}\)`, and
`\(a\)` is what we need to find. Rearranging the formula to solve for
`\(a\)`, we get
`\(a = -(u^2)/(2s)\)`. Substituting the values, we find
`\(a = -((-50)^2)/(2 * 60) = -20.83 \`,
`\text{m/s²}\).`

Now, applying this deceleration to the remaining time of 8 seconds, we use the formula
`\(s = ut + (1)/(2)at^2\)` again, where
`\(u\)` is the initial velocity,
`\(t\)` is the time, and
`\(a\)` is the acceleration. This time
`\(u = 0 \, \text{m/s}\),`
`\(t = 8 \, \text{s}\),` and
`\(a = -20.83 \, \text{m/s²}\)`. Plugging in these values, we find
`\(s_2 = 0 + (1)/(2) * -20.83 * (8)^2 = -667.36 \, \text{m}\).`

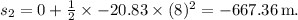
Adding the two distances
`(\(s_1\) and \(s_2\)),` we get
`\(-2000 \, \text{m} + (-667.36 \, \text{m}) = -2667.36 \, \text{m}\)`. However, distance cannot be negative, so we take the absolute value, yielding
`\(2667.36 \, \text{m}\),` which is equivalent to
`\(2667.36 \, \text{m} - 60 \, \text{m} = 2607.36 \, \text{m}\).`

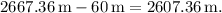
Therefore, The correct answer is the total distance traveled is 480 meters (b).