Question

Factor the given trinomial. If the trinomial cannot be factored, indicate “not factorable” 6v^5-18v^4-168v^3

Answer 1

The polynomial is given below as

`6v^5-18v^4-168v^3`

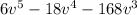
Step 1: Factor out the highest common factor which is

`6v^3`
`\begin{gathered} 6v^5-18v^4-168v^3=6v^3((6v^5)/(6v^3)-(18v^4)/(6v^3)-(168v^3)/(6v^3)) \\ 6v^5-18v^4-168v^3=6v^3(v^2-3v-28) \end{gathered}`

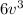
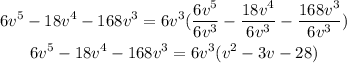
Step 2: Factorise the quadratic expression

`v^2-3v-28`

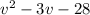
To factorize the quadratic expression, we will have to look for two factors that will multiply each other to give a -28, and then the same two factors will add up together to give -3

By try and error, we will have the two factors to be

`\begin{gathered} -7*+4=-28 \\ -7+4=-3 \end{gathered}`

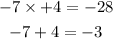
By replacing the two factors in the equation above, we will have

`\begin{gathered} v^2-3v-28=v^2-7v+4v-28 \\ \text{group the factors to have} \\ (v^2-7v)+(4v-28)=v(v-7)+4(v-7) \\ v^2-3v-28=(v-7)(v+4) \end{gathered}`

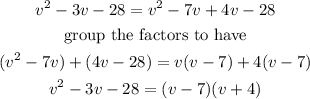
Hence,

`6v^5-18v^4-168v^3=6v^3(v-7)(v+4)`

Therefore,

The final answer is 6v³(v - 7)(v + 4)