Question

In the diagram, the square and the trapezium share a common side of length x cm. xcm. 6 cm -10cm The area of the square is equal to the area of the trapezium. Work out the value of x. Not to scale Refer to photo ​

Answer 1

The value of x, given that the square and the trapezium share a common side of length x cm, is 7.2 cm

How to work out the value of x in the diagram?

The value of x can be calculated as follow:

First, we shall obtain the area of the trapezium. Details below:

• Base side 1 (a) = x cm
• Base side 2 (b) = 10 cm
• Height (h) = 6 cm
• Area of trapezium (A) = ?

`A = (1)/(2)(a\ +\ b)h\\ \\A = (1)/(2)(x\ +\ 10)6\\\\A = (x\ +\ 10)3\\\\A = 3x\ +\ 30`

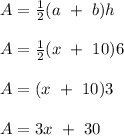
Next, we shall obtain the area of the square. This is shown below:

• Length (L) = x cm
• Area of square (A) = ?

A = L²

A = x²

Now, equate the area of the trapezium to the area of the square to determine the value of x. Details below:

• Area of trapezium = 3x + 30
• Area of square = x²

Area of square = Area of trapezium

x² = 3x + 30

Rearrange

x² - 3x - 30 = 0

Solving by formula method, we have:

• a = 1
• b = -3
• c = -30

`x = (-b\ \pm\ √(b^2\ -\ 4ac))/(2a) \\\\x = (-(-3)\ \pm\ √((-3)^2\ -\ (4\ *\ 1\ *\ -30)))/(2\ * 1)\\\\x = (3\ \pm\ √(9\ +\ 120))/(2)\\\\x = (3\ \pm\ √(129))/(2)\\\\x = (3\ +\ √(129))/(2)\ or\ (3\ -\ √(129))/(2)\\\\x = 7.2\ or\ -4.2`

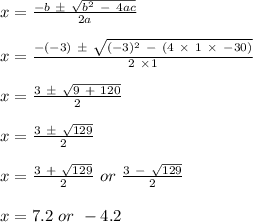
Since the measurement can not be negative, thus, the value of x is 7.2 cm