Question

How many miles would Christine need to drive for the two plans to cost the same?

A. 100 miles
B. 200 miles
C. 300 miles
D. 400 miles

Answer 1

The final answer is C. 300 miles. This is determined by equating the total costs of Plan A and Plan B and solving for the number of miles, resulting in the break-even point at 300 miles.

Step-by-step explanation:

To determine the number of miles Christine needs to drive for the two plans to cost the same, we can set up an equation based on the information provided. Let's denote the cost per mile for Plan A as
`\( A_m \)`and for Plan B as
`\( B_m \).`The total cost for each plan is the sum of a fixed cost and the cost per mile multiplied by the number of miles driven.

For Plan A:
`\( A_{\text{total}} = 50 + 0.40 * \text{miles} \)`

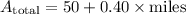
For Plan B:
`\( B_{\text{total}} = 30 + 0.60 * \text{miles} \)`

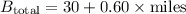
Now, we want to find the number of miles
`(\( \text{miles} \))`at which the total costs for both plans are equal:

`\[ 50 + 0.40 * \text{miles} = 30 + 0.60 * \text{miles} \]`

Solving for
`\( \text{miles} \), we get \( \text{miles} = (20)/(0.20) = 300 \).\\`

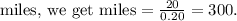
Therefore, Christine would need to drive 300 miles for the two plans to cost the same.

In summary, by equating the total costs for both plans and solving for the number of miles, we find that Christine needs to drive 300 miles for Plan A and Plan B to have equal costs. This break-even point is the key to determining when the two plans become financially equivalent.