Question

A car speeds up uniformly while rounding a turn. The car's angular speed increases from 0.54 radians per second to 0.96 radians per second as it turns through 1.40 radians. What is the car's angular acceleration? Include units in your answer. Answer must be in 3 significant digits.

Answer 1

Given data:

* The initial angular speed of the car is,

`\omega_i=0.54\text{ rad/s}`

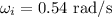
* The final angular speed of the car is,

`\omega_f=0.96\text{ rad/s}`

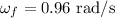
* The angular displacement of the car is,

`\theta=1.4\text{ radians}`

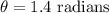
Solution:

By the kinematics equation, the angular acceleration of the car in terms of the angular displacement is,

`\omega^2_{\text{f}}-\omega^2_i=2\alpha\theta`

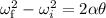
where,

`\alpha\text{ is the angular acceleration,}`

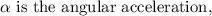
Substituting the known values,

`\begin{gathered} 0.96^2-0.54^2=2*\alpha*1.4 \\ \alpha=(0.96^2-0.54^2)/(2*1.4) \\ \alpha=(0.9216-0.2916)/(2.8) \\ \alpha=(0.63)/(2.8) \end{gathered}`

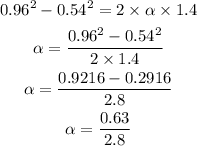
By simplifying,

`\alpha=0.225rads^(-2)`

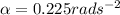
Thus, the angular acceleration of the car is 0.225 radians per second squared.