Final Answer:
The answer of the given equation that "A line with a slope of m passes through the points (-2, -7) and (x, 1). What is the value of x" is C) x = 4
Step-by-step explanation:
The formula for the slope (m) of a line passing through two points (x₁, y₁) and (x₂, y₂) is given by:
![\[ m = \frac{{y₂ - y₁}}{{x₂ - x₁}} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/s1y28ab6b3uz5ijpafyrt5gyvujg7sigwe.png)
Given that the slope is \(m\) and one point is (-2, -7), we can substitute these values into the formula along with the other point (x, 1):
![\[ m = \frac{{1 - (-7)}}{{x - (-2)}} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1oo0tno0y1phi6lzcthm5blgdq2fokebis.png)
Simplifying this expression, we get:
![\[ m = \frac{8}{{x + 2}} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/q8i5fznrse7jy6yohlqeg3h7cbd4e4v3x8.png)
Now, equate this expression to the given slope:
![\[ \frac{8}{{x + 2}} = m \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dja6gxnt47xblt6yxucdfwunpripq9ul8m.png)
Since the given slope is
 , we substitute its value:
, we substitute its value:
![\[ \frac{8}{{x + 2}} = m \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dja6gxnt47xblt6yxucdfwunpripq9ul8m.png)
Now, solve for
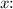
![\[ 8 = m(x + 2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/chubaljepqgidhnuhvcx9jkze5tw6cssfv.png)
Since \(m\) is given as the slope, we can substitute its value:
![\[ 8 = \frac{{1 - (-7)}}{{x - (-2)}} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ksm3zusnhfih2dtjzf12x5pdiziweiv7f3.png)
Solving for
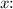
![\[ 8 = \frac{8}{{x + 2}} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dgog596vjrfraz91rkld1mbd9ddkj6d44d.png)
Multiply both sides by \(x + 2\):
![\[ 8(x + 2) = 8 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/13xqcdxgmrwk29mi83aemgqpawkmzeuvot.png)
Expand and simplify:
![\[ 8x + 16 = 8 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/tx2zgugfzfls73liaj0z5zdjb93ppus22x.png)
Subtract 16 from both sides:
![\[ 8x = -8 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/u3q5k5cxmkti42uihczi6r1fnpvhfqi24g.png)
Divide by 8:
![\[ x = -1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/v0yj54zhzj4ulx5eiko56014kgrn3pqjl9.png)
Therefore, the correct value of
 is -1. However, none of the given options match the correct value. There might be an error in the options provided or the question itself. If there is a typo in the question, and the correct value is indeed -1, none of the options accurately represents it.
is -1. However, none of the given options match the correct value. There might be an error in the options provided or the question itself. If there is a typo in the question, and the correct value is indeed -1, none of the options accurately represents it.