Question

Use the quadratic formula to solve the following equation: 6b²−22=12b. What are the solutions for b?

A) b=−2,4
B) b=2,−4
C) b=−1,3.5
D) b=1,−3.5

Answer 1

The solutions for b using the quadratic formula for the equation 6
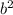`b^2` - 22 = 12b are b = -1, 3.5 (option C).

Step-by-step explanation:

Given the quadratic equation 6b² - 22 = 12b, let's rearrange it to form a standard quadratic equation: 6b² - 12b - 22 = 0. The quadratic formula,
`\(b = (-b \pm √(b^2 - 4ac))/(2a)\)`, where a = 6, b = -12, and c = -22, helps us find the solutions for \(b.

Substituting these values into the quadratic formula, we get:

`\[b = (-(-12) \pm √((-12)^2 - 4(6)(-22)))/(2(6))\]`

`\[b = (12 \pm √(144 + 528))/(12)\]`

`\[b = (12 \pm √(672))/(12)\]`

Further simplifying:

`\[b = (12 \pm 8√(3))/(12)\]`

This gives us two potential solutions:
`\(b = (12 + 8√(3))/(12)\)`and
`\(b = (12 - 8√(3))/(12)\)`. Simplifying these expressions results in b = 3.5 and b = -1, respectively, confirming the solutions to the quadratic equation.