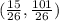Given the coordinates of two points P and Q, we can calculate the distance between them using the formula:
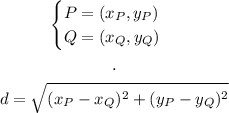
In this case, we want the smallest distance between a point in the curve and the point (0, 4)
Then, we know that there is a point that we can call Q = (x, y) that is the closest to the point (0, 4). We can write, using the distance formula:
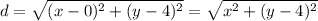
The equation given is:
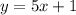
We want to rewrite the distance formula to include the equation of the curve. Since there is a term 'x²', we can solve the equation for x and square on both sides:
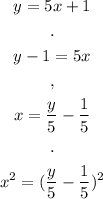
Now we can substitute in the distance equation:
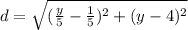
We can see that this is a distance function for any point of the curve to the point (0, 4). This is actually a function of y.
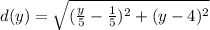
Now, we can apply calculus to find the minimum of this function. Let's take the first derivative:
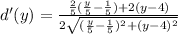
Simplify:
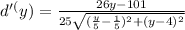
And since we want to find a minimum, we need to also calculate the second derivative:
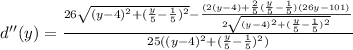
Simplify:
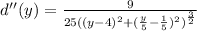
Now, we need to find the critical points of the function. The critical points are the x values where the first derivative is 0.
Then:
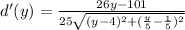
Is a quotient, For a quotient to be 0, the only way this is possible is for the numerator to be 0. Then:
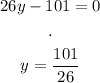
And now, to see if this critical point is a minimum, we evaluate it in the second derivative, if the second derivative is positive in this critical point, the function has a minimum at that point:
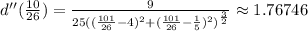
Then, the function d(y) has a minimum at y = 101/26
Now, we need to find the x coordinate of this point. We use the equation of the curve:
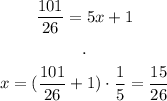
Thus, the answer to the point in the curve that is the closest to (0, 4) is: