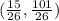Question

Find the point on the curve y=5x+1 closest to the point (0,4).

Answer 1

Given the coordinates of two points P and Q, we can calculate the distance between them using the formula:

`\begin{gathered} \begin{cases}P={(x_P},y_P) \\ Q={(x_Q},y_Q)\end{cases} \\ . \\ d=√((x_P-x_Q)^2+(y_P-y_Q)^2) \end{gathered}`

In this case, we want the smallest distance between a point in the curve and the point (0, 4)

Then, we know that there is a point that we can call Q = (x, y) that is the closest to the point (0, 4). We can write, using the distance formula:

`d=√((x-0)^2+(y-4)^2)=√(x^2+(y-4)^2)`

The equation given is:

`y=5x+1`

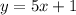
We want to rewrite the distance formula to include the equation of the curve. Since there is a term 'x²', we can solve the equation for x and square on both sides:

`\begin{gathered} y=5x+1 \\ . \\ y-1=5x \\ , \\ x=(y)/(5)-(1)/(5) \\ . \\ x^2=((y)/(5)-(1)/(5))^2 \end{gathered}`

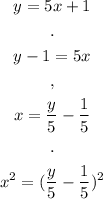
Now we can substitute in the distance equation:

`d=\sqrt{((y)/(5)-(1)/(5))^2+(y-4)^2}`

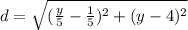
We can see that this is a distance function for any point of the curve to the point (0, 4). This is actually a function of y.

`d(y)=\sqrt{((y)/(5)-(1)/(5))^2+(y-4)^2}`

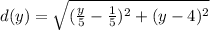
Now, we can apply calculus to find the minimum of this function. Let's take the first derivative:

`d^(\prime)(y)=\frac{(2)/(5)((y)/(5)-(1)/(5))+2(y-4)}{2\sqrt{((y)/(5)-(1)/(5))^2+(y-4)^2}}`

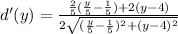
Simplify:

`d^(\prime)^(y)=\frac{26y-101}{25\sqrt{((y)/(5)-(1)/(5))^2+(y-4)^2}}`

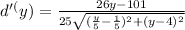
And since we want to find a minimum, we need to also calculate the second derivative:

`d^(\prime)^(\prime)(y)=\frac{26\sqrt{(y-4)^2+((y)/(5)-(1)/(5))^2}-\frac{(2(y-4)+(2)/(5)((y)/(5)-(1)/(5))(26y-101)}{2\sqrt{(y-4)^2+((y)/(5)-(1)/(5))^2}}}{25((y-4)^2+((y)/(5)-(1)/(5))^2)}`

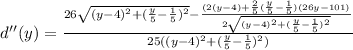
Simplify:

`d^(\prime)^(\prime)(y)=\frac{9}{25((y-4)^2+((y)/(5)-(1)/(5))^2)^{(3)/(2)}}`

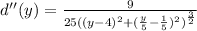
Now, we need to find the critical points of the function. The critical points are the x values where the first derivative is 0.

Then:

`d^(\prime)(y)=\frac{26y-101}{25\sqrt{(y-4)^2+((y)/(5)-(1)/(5))^2}}`

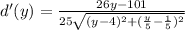
Is a quotient, For a quotient to be 0, the only way this is possible is for the numerator to be 0. Then:

`\begin{gathered} 26y-101=0 \\ . \\ y=(101)/(26) \end{gathered}`

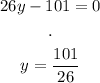
And now, to see if this critical point is a minimum, we evaluate it in the second derivative, if the second derivative is positive in this critical point, the function has a minimum at that point:

`d^(\prime)^(\prime)((10)/(26))=\frac{9}{25(((101)/(26)-4)^2+((101)/(26)-(1)/(5))^2)^{(3)/(2)}}\approx1.76746`

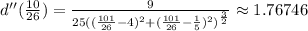
Then, the function d(y) has a minimum at y = 101/26

Now, we need to find the x coordinate of this point. We use the equation of the curve:

`\begin{gathered} (101)/(26)=5x+1 \\ . \\ x=((101)/(26)+1)\cdot(1)/(5)=(15)/(26) \end{gathered}`

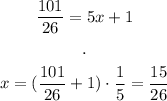
Thus, the answer to the point in the curve that is the closest to (0, 4) is:

`((15)/(26),(101)/(26))`