Question

Solve the problem by multiplying first.

Jamian bought a total of 35 bagels and donuts for a morning meeting. He paid a total of

$25.75. Each donut cost $0.55 and each bagel cost $1.20. The system of equations

b + d = 35

1.200 + 0.55d = 25.75 models this situation, where b is the number of bagels and d

is the number of donuts. How many of each did Jamian buy?

{ 1.200

Jamian bought

bagels and

donuts.

Answer 1

Number of bagels = 10

Number of donuts = 25

Explanation:

Let Number of bagels = b

Number of donuts = d

As given,

Each donut cost $0.55 and each bagel cost $1.20

⇒ Cost of d donuts = $0.55d

Cost of b bagels = $1.20b

Also given,

Jamian bought a total of 35 bagels and donuts

⇒ b + d = 35 ........(1)

Also,

He paid a total of $25.75.

⇒ 1.20b + 0.55d = 25.75 .........(2)

Now,

Multiply equation (1) by 1.20 , we get

1.20( b + d = 35 )

⇒1.20b + 1.20d = 42 ..........(3)

Now,

Subtract equation (2) from equation (3), we get

1.20b + 1.20d - ( 1.20b + 0.55d ) = 42 - 25.75

⇒1.20b + 1.20d - 1.20b - 0.55d = 16.25

⇒0.65d = 16.25

⇒d =
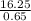`(16.25)/(0.65)` = 25

⇒d = 25

Put the value of d in equation (1) , we get

b + d = 35

⇒b + 25 = 35

⇒b = 35 - 25 = 10

⇒b = 10

∴ we get

Number of bagels = b = 10

Number of donuts = d = 25